კოსინუსების თეორემა

სამკუთხედი

კოსინუსების თეორემა — ტრიგონომეტრიის ერთ-ერთი თეორემა, რომლის თანახმადაც სამკუთხედის გვერდის კვადრატი უდრის დანარჩენი ორი გვერდის კვადრატების ჯამს ამ გვერდისა და მათ შორის მდებარე კუთხის კოსინუსის გაორკეცებული ნამრავლის გამოკლებით.

$c^2=a^2+b^2-2ab\cos \gamma$

$b^2=c^2+a^2-2ca\cos \beta$

$a^2=b^2+c^2-2bc\cos \alpha$

ისტორია

ბლაგვკუთხა სამკუთხედი ABC სიმაღლით BH

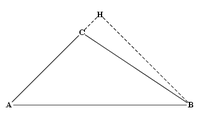
ბერძენი მათემატიკოსის, გეომეტრიის ფუძემდებლად წოდებული ევკლიდეს, „საწყისებში“, რომელიც ქრ.შ-მდე III საუკუნით თარიღდება, განხილულია კოსინუსების თეორემა ბლაგვკუთხა და მახვილკუთხა სამკუთხედებისთვის. ევკლიდეს დებულება შეიძლება, ნახაზიდან გამომდინარე, ასე გადმოვცეთ:

$A{B}^2=C{A}^2-C{B}^2+2\cdot CA\cdot CH$

ეს ფორმულა შეიძლება ჩაიწეროს, როგორც კოსინუსების თეორემა, რადგან

$CH=CB\cos (180^{\circ }-\gamma )=-CB\cos \gamma$

ევკლიდე ანალოგიურ დებულებას გადმოგვცემს მახვილკუთხა სამკუთხედებისთვისაც.
საინტერესოა ის, რომ ევკლიდეს დროს არ იყო შესწავლილი ალგებრა (კერძოდ, უარყოფითი რიცხვები) და ტრიგონომეტრიული ფუნქციები, ამიტომაც ევკლიდეს დებულებებს გეომეტრიული ელფერი დაჰკრავთ.
დასავლეთს კოსინუსების თეორემა ფრანსუა ვიეტმა გააცნო, რომელიც მან სავარაუდოდ დამოუკიდებლად აღმოაჩინა. თეორემამ დღევანდელი სახე XIX საუკუნის დასაწყისში მიიღო.

დამტკიცება

ვთქვათ, ABC სამკუთხედში B წვეროდან AC გვერდის მიმართ გავლებულია სიმაღლე BD. სიმაღლე შეიძლება მდებარეობდეს როგორც სამკუთხედის შიგნით (შემთხვევა 1), ისე ემთხვეოდეს მის გვერდს (შემთხვევა 2), ან მდებარეობდეს სამკუთხედის გარეთ (შემთხვევა 3):

ფაილი:Kos teorema shemtkhveva 1.svg

შემთხვევა 1

შემთხვევა 1: D წერტილი A და C წერტილებს შორისაა.
BCD სამკუთხედიდან

$B{C}^2=B{D}^2+D{C}^2$

ABD სამკუთხედიდან

$B{D}^2=A{B}^2-A{D}^2$

მაშინ

$B{C}^2=A{B}^2-A{D}^2+D{C}^2=A{B}^2-A{D}^2+(AC-AD{)}^2=A{B}^2-A{D}^2+A{C}^2-2AC\cdot AD+A{D}^2=A{B}^2+A{C}^2-2AC\cdot AD$

იმის გათვალისწინებით, რომ

$AD=AB\cos A$

მიიღება:

$B{C}^2=A{B}^2+A{C}^2-2AB\cdot AC\cos A$

ფაილი:Kos teorema shemtkhveva 2.svg

შემთხვევა 2

შემთხვევა 2: BD სიმაღლე ერთ-ერთ გვერდს ემთხვევა (ABC სამკუთხედი მართკუთხაა).
მაშინ, პითაგორას თეორემის თანახმად,

$B{C}^2=A{B}^2+A{C}^2$

რადგან

$\cos 90^{\circ }=0$

ეს ტოლობა ასეც შეიძლება ჩაიწეროს:

$B{C}^2=A{B}^2+A{C}^2-2AB\cdot AC\cos A$

ფაილი:Kos teorema shemtkhveva 3.svg

შემთხვევა 3

შემთხვევა 3: C წერტილი A და D წერტილებს შორისაა.
CBD სამკუთხედიდან:

$B{C}^2=B{D}^2+C{D}^2$

ABD სამკუთხედიდან

$B{D}^2=A{B}^2-A{D}^2$

მაშინ

$B{C}^2=A{B}^2-A{D}^2+C{D}^2=A{B}^2-A{D}^2+(AD-AC{)}^2=A{B}^2-A{D}^2+A{D}^2-2AD\cdot AC+A{C}^2=A{B}^2+A{C}^2-2AD\cdot AC$

იმის გათვალისწინებით, რომ

$AD=AB\cos A$

მიიღება:

$B{C}^2=A{B}^2+A{C}^2-2AB\cdot AC\cos A$

თეორემა დამტკიცებულია ყველა შესაძლო შემთხვევისთვის.

გამოყენება

კოსინუსების თეორემა გამოიყენება სამკუთხედების ამოხსნისას (მისი ყველა ელემენტის პოვნისას).
მაგალითად, როდესაც მოცემულია სამკუთხედის ყველა გვერდი, შეგვიძლია ვიპოვოთ მისი ყველა კუთხე. კოსინუსების თეორემიდან ვიღებთ, რომ

$\cos \alpha =\frac{b^2+c^2-a^2}{2bc}$

$\cos \beta =\frac{a^2+c^2-b^2}{2ac}$

$\cos \gamma =\frac{a^2+b^2-c^2}{2ab}$

ცხადია, კოსინუსების თეორემას ვიყენებთ მაშინაც, როდესაც ცნობილია სამკუთხედის ორი გვერდი და მათ შორის მდებარე კუთხე. ამ დროს მესამე გვერდი იქნება:

$c=\sqrt{a^2+b^2-2ab\cos \gamma }$

ტოლფერდა სამკუთხედის შემთხვევა

როცა a=b, ანუ როდესაც სამკუთხედი ტოლფერდაა, სამკუთხედის წვეროს პოვნის ფორმულა მნიშვნელოვანწილად მარტივდება.
როგორც ვიცით

$\cos \gamma =\frac{a^2+b^2-c^2}{2ab}$

რადგან

$a^2+b^2=2a^2=2ab$

მაშინ

$\cos \gamma =\frac{2ab-c^2}{2ab}=1-\frac{c^2}{2ab}=1-\frac{c^2}{2a^2}$

იხილეთ აგრეთვე

• სინუსების თეორემა
• ტანგესების თეორემა

ლიტერატურა

• ქართული საბჭოთა ენციკლოპედია, ტ. 5, თარგი:ადგილის მითითება ბიბლიობმულებში, 1980. — გვ. 683.